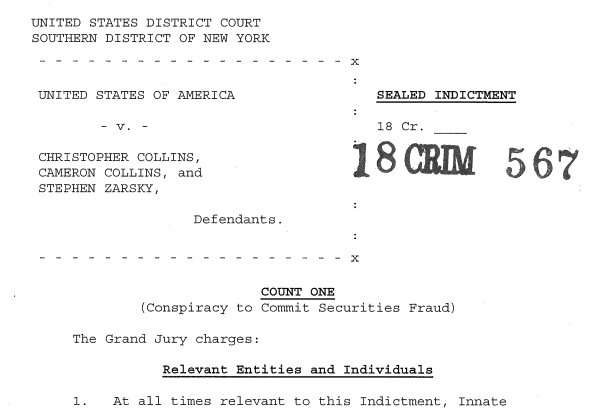
Federal prosecutors indicted Rep. Christopher Collins on Wednesday, charging the third term Republican with securities fraud, wire fraud and making false statements. The charges relate to insider trading associated with a biotech firm.
Collins represents New York's 27th congressional district, a conservative district between Buffalo and Rochester. Collins won reelection by 34% in 2016, and was unopposed in the state's primary in late June. Sabato's Crystal Ball has modified its 2018 election rating from safe to likely Republican on news of the indictment.