Election News

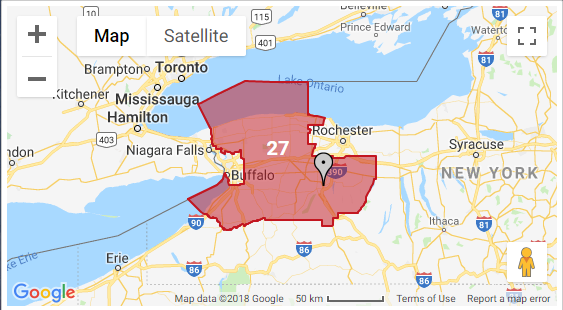
On the advice of his attorneys, GOP Rep. Chris Collins (NY-27) will remain on the November ballot. Collins was indicted for insider trading back in August and he subsequently suspended his campaign. However, efforts to remove him from the ballot - a tough thing to do in New York state - have proven unsuccessful.  

The change further improves the Democratic outlook for this previously safe Republican stronghold between Rochester and Buffalo. Donald Trump won here by nearly 25% in 2016, his largest margin of victory in any of the state's 27 congressional districts. Kyle Kondik, of Sabato's Crystal Ball, indicates the race will move from Likely to Leans Republican.

The 2018 primary season wraps up Thursday with the New York primaries for state and local offices. The state's primaries for federal offices were held in late June.

We're following the Democratic primaries for governor and attorney general. Polls close at 9:00 PM Eastern Time. Live results will be available on this page after that time. Reload for the latest totals.

Not sure where to vote? Look up your polling place.

Rhode Island Primaries

Rhode Island holds its 2018 primaries on Wednesday, September 12th. Polls close at 8:00 PM Eastern Time. Live results will be available on this page after that time. Reload for the latest totals.

Not sure where to vote? Look up your polling place.

The final week of the 2018 primary calendar has arrived. Three days, three Northeastern states; although for one of those it is the completion of a split primary.  New Hampshire kicks things off Tuesday; see below for a preview and live results. Rhode Island holds its primaries on Wednesday. The party primaries for governor are what we'll be watching there. New York wraps things up Thursday, with primaries for non-Federal offices. For our purposes, that is just the high-profile Democratic gubernatorial primary featuring incumbent Gov. Andrew Cuomo and actress/activist Cynthia Nixon.

New Hampshire Primaries

Most New Hampshire polls close at 7:00 PM Eastern Time, with the remainder closing at 8:00 PM. Live results will be available on this page after that time. Reload for the latest totals.

Florida Rep. Ron DeSantis has resigned from Congress to focus on his campaign to be the state's next governor. DeSantis asked that his resignation be effective September 1, although his letter to Speaker Ryan is dated September 10. 

DeSantis recently won the Republican nomination for governor, helped along by the strong support of President Trump. He will meet Democratic Tallahassee Mayor Andrew Gillum in one of the marquee races this November. Incumbent Gov. Rick Scott (R) is termed out; he is running for Senate against incumbent Sen. Ben Nelson (D).

Delaware Primaries

Delaware polls close at 8:00 PM Eastern Time; Live results will be available on this page after that time. Reload for the latest totals.

Not sure where to vote? Look up your polling place.

Ayanna Pressley, who serves on the Boston City Council, defeated 10-term Rep. Michael Capuano in Tuesday's Massachusetts primary. The district, once represented by John F. Kennedy, is one of the most liberal in the country. As with Capuano in 2016, Pressley will have no Republican opponent in November. Capuano is the fourth House member to be ousted in a party primary this year.

All other U.S. House incumbents that faced primary challenges were victorious, and are expected to win re-election in November. In the 3rd district, where Rep. Niki Tsongas is retiring, a 10-way primary remained undecided. Daniel Koh and Lori Trahan were separated by fewer than 100 votes as of Wednesday AM.

Massachusetts Primaries

Massachusetts polls close at 8:00 PM Eastern Time; Live results will be available on this page after that time. Reload for the latest totals.

Not sure where to vote? Look up your polling place.

Choose a state below for all primary results

Florida

A New York Times headline sums it up nicely:  "A Black Progressive and a Trump Acolyte Win Florida Governor Primaries". Voters in both parties bypassed the establishment candidate. Democrats selected Tallahassee Mayor Andrew Gillum, who upset former Rep. Gwen Graham. Republicans followed the endorsement of President Trump, choosing Rep. Ron DeSantis. The general election here thus takes on echoes of neighboring Georgia, both gubernatorial races "between left-leaning African-Americans banking on the region’s new, diversifying electorate, and ardent, Trump-style nationalists."